[数论]bzoj4173 数学

发表于 | 更新于: | 分类于 ，

依旧是一道欧拉函数qwq
可以快乐打表
或者蜜汁推导orz…

题意

$S(n,m)$为满足$m mod k+n mod k>=k$的所有整数$k$组成的集合，求：

n,m<=10^15

输入输出

输入：
m和n

输出：
如题

input
5 6

output
240

题解

由于菜到真实，并没有想到正解，于是大佬：你打表啊qwq

划水做法

下面是打表代码 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
#include <bits/stdc++.h>
using namespace std;

int phi(int x){
    int ret=x;
    for(int i=2;i*i<=x;i++){
        if(x%i==0) ret-=ret/i;
        while(x%i==0) x/=i;
    }
    if(x>1) ret-=ret/x;
    return ret;
}

int main(){
    for(int i=1;i<=10;i++){
        for(int j=1;j<=10;j++){
            int sum=0;
            for(int k=1;k<=i+j;k++){
                if((i%k)+(j%k)>=k) sum+=phi(k);
            }
            cout<<setw(4)<<sum;
        }
        cout<<endl;
    }
    return 0;
}

于是发现了很神奇的规律…

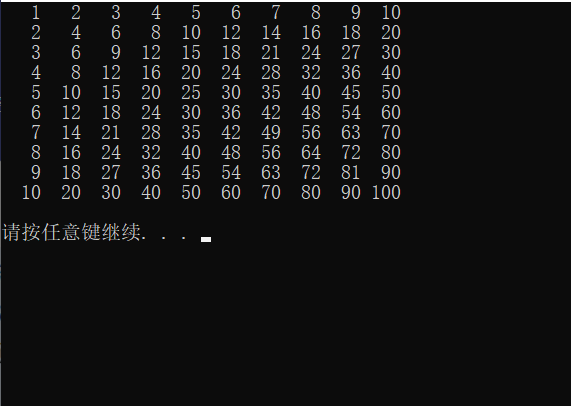
图丢了qwq

于是令人头疼的$\sum_{k\in S(n,m)}\phi(k)$就变成了$n* m$了qwqwq
打表真香
代码如下

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int mod=998224353;

ll phi(ll x){
    ll ret=x;
    for(ll i=2;i*i<=x;i++){
        if(x%i==0) ret-=ret/i;
         while(x%i==0) x/=i;
    }
    if(x>1) ret-=ret/x;
    return ret;
}

int main(){
    ll a,b;scanf("%lld%lld",&a,&b);
    cout<<(((phi(a)*phi(b))%mod)*((a*b)%mod))%mod<<endl;
    return 0;
}

正经推导

令$m=p_1k+q_1$，$n=p_2k+q_2$，因此：

所以有：

又因为：

所以：

于是