树剖,树剖好吃吗?
这里是树链剖分
小菜鸡在长时间划水之后终于似乎看懂了树链剖分(⁄ ⁄•⁄ω⁄•⁄ ⁄)
部分转自 ivanovcraft带师 和 百度百科。
概念
(悄悄说)之前看了好多好多博客,大概只是知道树链剖分的实现,但并不了解树链剖分存在的意义……
(继续悄悄说)所以毛毛雨去查了一下百度百科(⁄ ⁄•⁄ω⁄•⁄ ⁄),感觉百度百科简直是良心定义!!
以下内容摘自百度百科
- 树路径信息维护算法。
- 将一棵树划分成若干条链,用数据结构(树状数组、BST、SPLAY、线段树等)去维护每条链,
复杂度为O(logN)。- 其实本质是一些数据结构/算法在树上的推广
以后数据结构不仅仅可以维护线段,还可以用来维护树啦!!
(有点像从一维升级成二维了诶!)
一些基本定义
- 重结点:子树结点数目最多的结点;
- 轻节点:父亲节点中除了重结点以外的结点;
- 重边:父亲结点和重结点连成的边;
- 轻边:父亲节点和轻节点连成的边;
- 重链:由多条重边连接而成的路径;
- 轻链:由多条轻边连接而成的路径;
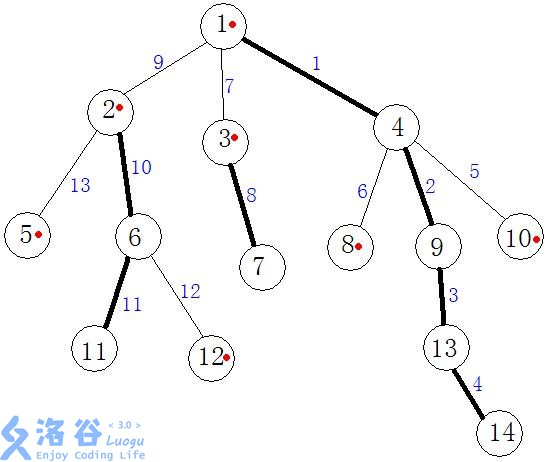
如图加粗的链为重链,标红点的为重链起点(即下文的top值)。
下面是个人理解(溜):重链为最长链,所有节点都能跳到重链上,并且跳的次数最少。其实随便选链进行剖分也是可以的,但选重链是最方便的~
然后有一些奇奇怪怪的性质:
- 轻边(u,v),size(v)<=size(u)/2。
- 从根到某一点的路径上,不超过O(logN)条轻边,不超过O(logN)条重路径。
实现过程
定义
要实现树链剖分,要记录下面的值
| 名称 | 解释 |
|---|---|
| f[u] | 保存结点u的父亲节点 |
| d[u] | 保存结点u的深度值 |
| size[u] | 保存以u为根的子树节点个数 |
| son[u] | 保存重儿子 |
| rk[u] | 保存当前dfs标号在树中所对应的节点 |
| top[u] | 保存当前节点所在链的顶端节点 |
| id[u] | 保存树中每个节点剖分以后的新编号(DFS的执行顺序) |
预处理
实现方式是进行两遍dfs
第一遍:
- 对于一个点,求出他所在子树大小,并找到它的重儿子(size、son数组)
- 记录它的父亲及深度(f、d数组)

第二遍:
- 连接重链,同时标记每一个节点的dfs序,并且为了用数据结构来维护重链,我们在dfs时保证一条重链上各个节点dfs序连续(即处理出数组top,id,rk)
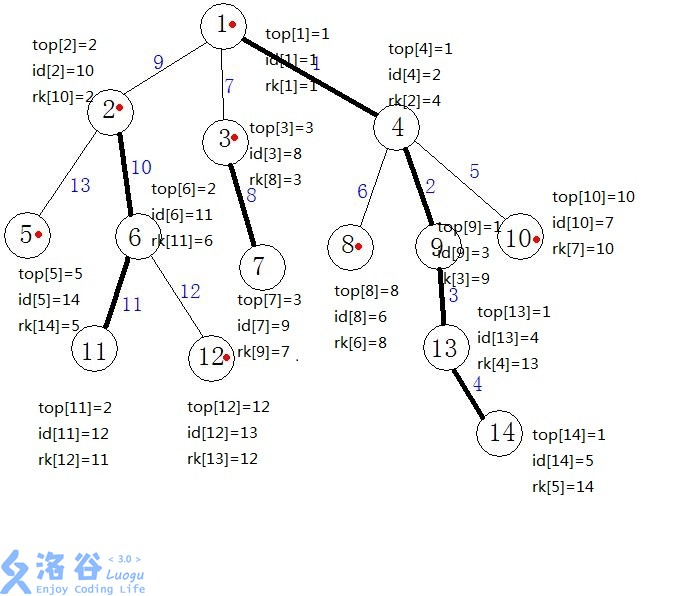
操作
- 如果两点位于不同重链,则将深度大的节点跳到所在重链顶端,并用数据结构维护这条重链的信息,然后沿轻链跳到当前节点的父亲节点。
- 如果两点位于同一重链,则统计这两点之间的信息。
然后一起来看题目鸭!
下面是愉快的贴代码部分啦QWQ
题目是洛谷p3384 树链剖分模板题。题目在这里!
1 |
|
一个很不正经的后记
仔细看了大佬们的博客并很认真地整理出来,对树剖也有了更深的认识。
然后毛毛雨的第一篇博客大功告成啦!!
虽然格式排版暂时还莫得,但是毛毛雨后期会调的啦!!况且都这么晚了╭(╯^╰)╮
不如……晚安!(*๓´╰╯`๓)♡