[2020杭电多校]第四场

发表于 | 更新于:

多校翻车场……

  • 1011 憨批签到题
  • 1002 队友写的一道水题qwq
  • 1005 一道简单dp
  • 1004 简单最短路，代码写出锅好久QAQ
  • 1007 经典二分图，然而憨憨地用了匈牙利，超时了好久……

1011 Kindergarten Physics

题目链接http://acm.hdu.edu.cn/showproblem.php?pid=6812

题意

给两个行星的质量a,b，距离d，问t时间后的距离。

盲目分析

由于a和b的单位都是km，且t只有100s，所以初始100s位置变化可以忽略不记，直接输出d即可QAQ
这个思路居然想了这么久，（最后还是听德芙讲的qwq）被自己菜哭QAQ

少的可怜的代码

1
2
3
4
5
6
7
8
9
10
11
12
#include <bits/stdc++.h>
using namespace std;

int main(){
    int t;scanf("%d",&t);
    while(t--){
        int a,b,d,t0;
        scanf("%d%d%d%d",&a,&b,&d,&t0);
        printf("%.6f\n",d*1.0);
    }
    return 0;
}

1002 Blow up the Enemy

题目链接http://acm.hdu.edu.cn/showproblem.php?pid=6803

题意

不知道，队友写的，听说是个水题qwq

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
#include<stdio.h>
#include<iostream>
#include<algorithm>
using namespace std;
double x[1005];
int main()
{
    int t;
    scanf("%d",&t);
    while(t--)
    {
        int n;
        long long int a,d;
        scanf("%d",&n);
        for(int i=0;i<n;i++)
        {
            scanf("%lld%lld",&a,&d);
            if(100%a==0)
                x[i]=(100/a-1)*1.0*d;
            else
                x[i]=1.0*(100/a)*d;
        }
        sort(x,x+n);
        long long int ans=1;
        for(int i=1;i<n;i++)
        {
            if(x[i]==x[i-1])
                ans++;
            else
                break;
        }
        printf("%lf\n",1.0*(n-ans)/n+0.5*ans/n);
    }
    return 0;
}

1005 Equal Sentences

题目链接 http://acm.hdu.edu.cn/showproblem.php?pid=6806

题意

懒得概括QAQ，反正是个dp，推推就出来了qwq

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
#include<stdio.h>
#include<iostream>
#include<cstring>
using namespace std;
const long long int mod=1e9+7;
char s1[20],s2[20];
long long int f[100005];
int main()
{
    int t;
    scanf("%d\n",&t);
    while(t--)
    {
        int n;
        scanf("%d\n",&n);
        if(n==1)
        {
            scanf("%s",s1);
            printf("1\n");
            continue;
        }
        else
            if(n==2)
            {
                scanf("%s%s",s1,s2);
                if(strcmp(s1,s2))
                {
                    printf("2\n");
                }
                else
                {
                    printf("1\n");
                }
                continue;
            }
        
        scanf("%s%s",s1,s2);
        if(strcmp(s1,s2))
        {
            f[1]=1;
            f[2]=2;
        }
        else
        {
            f[1]=1;
            f[2]=1;
        }
//        printf("%lld %lld\n",f[1],f[2]);
        for(int i=3;i<=n;i++)
        {
            scanf("%s",s1);
//            printf("%s %s\n",s1,s2);
            if(strcmp(s1,s2))
            {
                f[i]=(f[i-1]+f[i-2])%mod;
            }
            else
            {
                f[i]=f[i-1];
            }
//            printf("%lld\n",f[i]);
            strcpy(s2,s1);
        }
        printf("%lld\n",f[n]);
    }
    return 0;
}

1004 Deliver the Cake

题目链接 http://acm.hdu.edu.cn/showproblem.php?pid=6805

题意

一个人要从一个村子提蛋糕到另一个村子，经过有些村子只能用左手提蛋糕，标记为”L”，经过一些村子只能用右手提蛋糕，标记为”R”，还有些村子左右手都可以，标记为”M”。蛋糕换手需要花费x的时间。
有n个村庄，m条无向边，一个人从s村子走到t，问花费的最短时间

思路

L和L，或R和R的距离直接设为d，R和L的距离设为d+x。
如果有M，将M拆为两个点ML和MR，将ML和MR连起来，距离为x，然后将隔壁的L与ML连，距离为d，隔壁的R和MR连，距离为d。之后跑一遍最短路就可以了。
然后再搞个超级源和超级汇，方便解决起点和终点是M的情况。

代码

注意nxt数组要和边的大小一样，否则会超时QAQ

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
ll first[200005], nxt[1000005];
ll d[200005];
ll tot = 0;
bool used[200005];
struct edge
{
    ll  to;
    ll cost;
}es[1000005];
struct qaq{
    ll num;
    ll d;
};
bool operator < (qaq a, qaq b)
{
    return a.d > b.d;
}
priority_queue <qaq> q;

void build(ll f, ll t, ll d)
{
    es[++tot] = (edge){t,d};
    nxt[tot] = first[f];
    first[f] = tot;
}

void dijkstra(ll s)
{
    q.push((qaq){s, 0});
    d[s] = 0;
    used[s] = 1;
    while (!q.empty())
    {
        ll now = q.top().num;
        q.pop();
        used[now] = 1;
        for (ll i = first[now]; i != -1; i = nxt[i])
        {
            ll v = es[i].to;
            if (d[v] > d[now] + es[i].cost)
            {
                d[v] = d[now] + es[i].cost;
                if (!used[v])
                {
                    q.push((qaq){v, d[v]});
                }
            }
        }
    }
}
char S[100005];

int main()
{
    ll T;
    scanf("%lld",&T);
    while(T--){
        ll n,m,s,qwq,x;
        scanf("%lld%lld%lld%lld%lld\n",&n,&m,&s,&qwq,&x);
        scanf("%s",S+1);
        tot=0;
        ll tt=2*n+1;
        for(ll i=0;i<=tt;i++){
            d[i]=1e16;
            first[i]=-1;
            used[i]=0;
        }
        for(ll i=1;i<=n;i++){
            if(S[i]=='M'){
               build(i,i+n,x);//首先加一条自己左手到右手的边
               build(i+n,i,x);
            }
        }
        
        for (ll i = 1; i <= m; i++)
        {
            ll f, t, d;
            scanf("%lld%lld%lld", &f, &t, &d);
            if(S[f]=='M')//它是两只手都能用的点
            {
                if(S[t]=='L'){
                    build(f,t,d);
                    build(t,f,d);
                }
                else if(S[t]=='R'){
                    build(f+n,t,d);
                    build(t,f+n,d);
                }
                else{
                    build(f,t,d);
                    build(t,f,d);
                    build(f+n,t+n,d);
                    build(t+n,f+n,d);
                }
            }
            else if(S[f]=='L'){
                if(S[t]=='L'){
                    build(f,t,d);
                    build(t,f,d);
                }
                else if(S[t]=='R'){
                    build(f,t,d+x);
                    build(t,f,d+x);
                }
                else{
                    build(f,t,d);
                    build(t,f,d);
                }
            }
            else if(S[f]=='R'){
               if(S[t]=='L'){
                   build(f,t,d+x);
                   build(t,f,d+x);
               }
               else if(S[t]=='R'){
                   build(f,t,d);
                   build(t,f,d);
               }
               else{
                   build(f,t+n,d);
                   build(t+n,f,d);
               }
           }
        }
        build(0,s,0);
        if(S[s]=='M') build(0,s+n,0);
        build(qwq,2*n+1,0);
        if(S[qwq]=='M') build(qwq+n,1+2*n,0);
        dijkstra(0);
        //for(int i=0;i<n*2+2;i++) cout<<d[i]<<endl;
        printf("%lld\n",d[2*n+1]);
    }
    return 0;
}

1007 Go Running

题目链接 http://acm.hdu.edu.cn/showproblem.php?pid=6808

题意

一些人在一条直线上跑步，可以从任意起点往左跑或往右跑任意一段时间，速度都为1，现在给出一些组数据t和x，表示在t时刻x位置有人（可能有多个人），问至少多少人能满足上述条件。

思路

最大匹配等于最小点覆盖
画一个x-t图像可以看出来，每个点都可以延展到y轴上表示相应的两个点。所以对于给的某个点，要么是从左上方延展过来的，要么是从左下方延展过来的。到底该怎么选才能保证人数最少？这就用到了最小点覆盖，比如说x=1，t=2，可以是x0=3或者是x0=-1来的，那么我们就构建二分图，让3连接-1，最小点覆盖一定会最优的选择这个边上的至少一个点。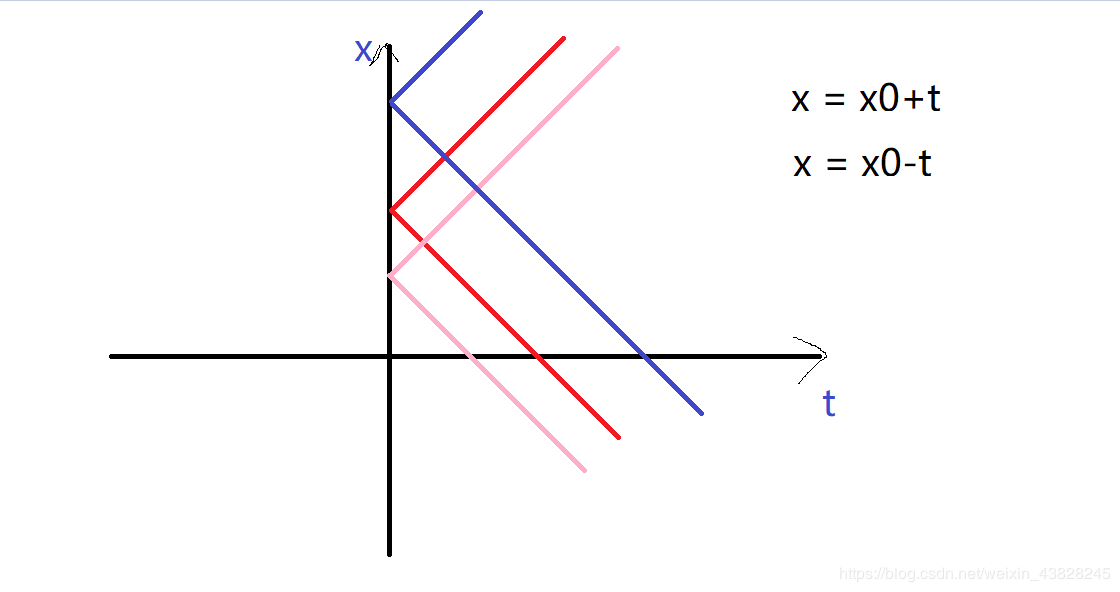
upload successful
然而匈牙利超时了QAQ
下面是用网络流过的代码qwq

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
#include<bits/stdc++.h>
using namespace std;
const int maxn=400010;
const int inf=0x3f3f3f3f;
struct edge{
    int to,flow,rev;
    edge(int to_,int flow_,int rev_){
        to=to_;
        flow=flow_;
        rev=rev_;
    }
};
int n,lsz,rsz;
vector<edge> gpe[maxn];
int dep[maxn];
bool vis[maxn];
bool bfs(int st,int ed) {
    for(int i=0;i<=lsz+rsz+1;i++) dep[i]=0;
    //memset(dep, 0, sizeof dep);
    queue<int> q;
    q.push(st);
    dep[st] = 1;
    while(!q.empty()) {
        int u = q.front();
        q.pop();
        for(int i=0;i<gpe[u].size();i++) {
            int v = gpe[u][i].to;
            if( dep[v] || gpe[u][i].flow <= 0) continue;
            dep[v] = dep[u] + 1;
            q.push(v);
        }
    }
    return dep[ed];
}
int dfs(int u,int flow,int ed){
    if(u == ed) return flow;
    int add = 0;
    for(int i=0;i<gpe[u].size();i++) {
        int v = gpe[u][i].to;
        if(dep[v] != dep[u] + 1) continue;
        if(!gpe[u][i].flow) continue;
        int tmpadd = dfs(v, min(gpe[u][i].flow, flow - add),ed);
        gpe[u][i].flow -= tmpadd;
        gpe[v][gpe[u][i].rev].flow+=tmpadd;
        add += tmpadd;
    }
    return add;
}
int dinic(int st,int ed){
    int max_flow = 0;
    while (bfs(st,ed)){
        max_flow += dfs(st,inf,ed);
    }
    return max_flow;
}

void addedge(int u,int v,int w){
    gpe[u].push_back(edge(v,w,gpe[v].size()));
    gpe[v].push_back(edge(u,0,gpe[u].size()-1));
}

int p[100005],x[100005];
int aa[200005];
int l[200005],r[100005];
int main(){
    int T;
    scanf("%d",&T);
    while(T--)
    {
        scanf("%d",&n);
        for(int i = 0; i < n; i++)
        {
            scanf("%d%d",&p[i],&x[i]);
            l[i]=x[i]-p[i];
            r[i]=x[i]+p[i];
        }
        sort(l,l+n);
        sort(r,r+n);
        lsz=unique(l,l+n)-l;
        rsz=unique(r,r+n)-r;
        for(int i = 0; i <=lsz+rsz+1; i++)
            gpe[i].clear();
        for(int i = 1; i <=lsz; i++)
        {
            addedge(0,i,1);
        }
        for(int i = 1; i <=rsz; i++)
        {
            addedge(i+lsz,lsz+rsz+1,1);
        }

        for(int i = 0; i < n; i++)
        {
            int pos1 = lower_bound(l,l+lsz,x[i]-p[i])-l+1;
            int pos2 = lower_bound(r,r+rsz,x[i]+p[i])-r+1;
            addedge(pos1,pos2+lsz,1);
        }
        printf("%d\n",dinic(0,lsz+rsz+1));
    }
    return 0;
}