扩展欧拉定理
题意:
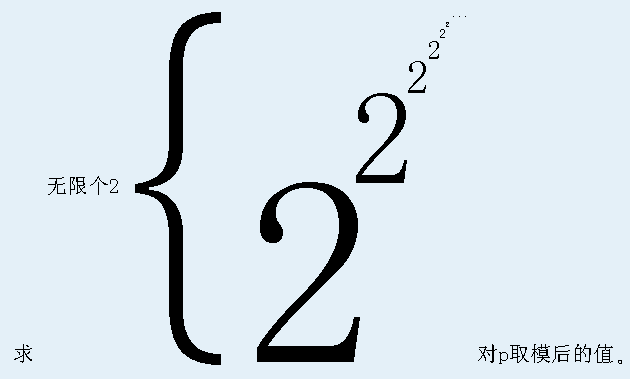
输入及输出
Input
接下来T行,每行一个正整数p,代表你需要取模的值
Output
T行,每行一个正整数,为答案对p取模后的值
Sample Input
3
2
3
6
Sample Output
0
1
4
HINT
对于100%的数据,T<=1000,p<=10^7
题解
令$m=2^{2^{2^{…}}}$,即求$m%p$。
考虑到m和p不一定互质,易想到扩展欧拉函数:
因此,令$f(p)=m\%p$,则有
于是可以递归求解,复杂度约为$O(\sqrt p * \log p)$1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
using namespace std;
int qpow(int a,int b,int mod){
int ans=1;
while(b){
if(b&1){
ans*=a;ans%=mod;
}
a*=a;a%=mod;
b>>=1;
}
return ans%mod;
}
int phi(int x){
int ret=x;
for(int i=2;i*i<=x;i++){
if(x%i==0) ret-=ret/i;
while(x%i==0) x/=i;
}
if(x>1) ret-=ret/x;
return ret;
}
int solve(int p){
if(p==1) return 0;
int pp=phi(p);
int res=solve(pp)+pp;
return (1<<res)%p;
}
int main(){
int t;scanf("%d",&t);
while(t--){
int num;scanf("%d",&num);
printf("%d\n",solve(num));
}
return 0;
}