qwq

标量、向量、矩阵和张量

标量单独的数
向量：一列数
$\boldsymbol x=\left[ \begin{matrix} x_1 \\\\ x_2 \\\\ x_3\\\\ \vdots\\\\ x_n \end{matrix} \right]$

可以把向量看作空间中的点，每个元素是不同坐标轴上的坐标。

索引：定义$S={ 1,3,6}$，$\boldsymbol xS$指定$x_1,x_3,x_6$，—表示补集的索引，$\boldsymbol x{—S}$表示$\boldsymbol x$中除$x_1,x_3,x_6$中的元素构成的向量。

矩阵：二维数组

索引：$A_{m,n}$

$\boldsymbol A{i,:}$表示$\boldsymbol A$ 的第$i$行，$\boldsymbol A{:,i}$表示$\boldsymbol A$的第$i$列。
$\left[ \begin{matrix} A_{1,1}&A_{1,2} \\\\ A_{2,1}&A_{2,2} \\\\ \end{matrix} \right]$
$f(\boldsymbol A)_{i,j}$：$f$作用在$\boldsymbol A$上输出的矩阵的第i行第j列元素
张量：超过二维的数组

转置：以对角线为轴的镜像

$(\boldsymbol{A}^{T})_ {i, j}=A_{j, i}$

矩阵相加：$\boldsymbol D=a\cdot \boldsymbol B+c$

矩阵和向量相加：$\boldsymbol C=\boldsymbol A+\boldsymbol b$，其中$C{i,j}=A{i,j}+b_j$ (广播)

矩阵和向量相乘

矩阵乘积：$\boldsymbol C=\boldsymbol {AB}$

元素对应乘积（Hadamard乘积）：$\boldsymbol A \odot \boldsymbol B$

两个维数相同的向量$\boldsymbol x$和$\boldsymbol y$的点积可以看作矩阵乘积$\boldsymbol x^T \boldsymbol y$。因此矩阵乘积可以看作第$i$行第$j$列的点积。

运算性质：

分配律：$\boldsymbol A(\boldsymbol B+\boldsymbol C)=\boldsymbol{AB}+\boldsymbol{AC}$

结合律：$\boldsymbol A(\boldsymbol{BC})=(\boldsymbol{AB})\boldsymbol C$

不满足交换律。

点积：$\boldsymbol x^{\top}\boldsymbol y=\boldsymbol y^{\top}\boldsymbol x$

转置：$(\boldsymbol{AB})^{\top}=\boldsymbol {B^{\top}A^{\top}}$

线性方程组：$\boldsymbol {Ax}=\boldsymbol b$

单位矩阵和逆矩阵

单位矩阵 $\boldsymbol In$：任意向量和单位矩阵相乘都不会改变。

$\forall\boldsymbol x\in\mathbb{R}^n,\boldsymbol{I_nx}=\boldsymbol x$

结构：

$\left[ \begin{matrix} 1&0&0 \\\\ 0&1&0 \\\\ 0&0&1\\\\ \end{matrix} \right]$

矩阵逆：$\boldsymbol A^{-1}$

$\boldsymbol {A^{-1}A}=\boldsymbol I_n$

逆矩阵主要作为理论工具使用，因为精度有限。

线性相关和生成子空间

对于$\boldsymbol {Ax}=\boldsymbol b$，如果有解，则一定存在一个解或无穷多解，不存在多余一个但少于无穷多解的情况。

可以将$\boldsymbol A$的列向量看作从原点出发的不同方向，确定有多少种方法可以到达向量$\boldsymbol b$，向量$\boldsymbol x$表示沿这些方向走多远。

线性组合：

$\boldsymbol {Ax}=\sum_ix_i\boldsymbol A_{:,i}$

生成子空间：原始向量线性组合后能达到的点的集合。

列空间（值域）：某矩阵列向量的生成子空间。

使$\boldsymbol {AX}=\boldsymbol b$对于任意向量$b\in\mathbb{R}^m$都有解，要$\boldsymbol A$的列空间构成$\mathbb{R}^m$，则$\boldsymbol A$至少有m个线性无关的列，否则只有当向量$\boldsymbol b$在n维平面上时有解。

若要矩阵可逆，还要保证对于每一个$\boldsymbol b$最多有一个解，因此矩阵最多有m个列向量。

因此这个可逆的矩阵必须为方阵且所有向量为线性无关。

奇异：列向量线性相关的方阵。

$\boldsymbol{A^{-1}A}=\boldsymbol{AA^{-1}}=\boldsymbol I$

范数

范数：衡量向量大小,表示从原点到点$\boldsymbol x$的距离。

$L^p$范数定义：

$||\boldsymbol x||_p=(\sum_i|x_i|^p)^{\frac 1p}$

$L^2$范数：p=2，欧几里得范数，$||\boldsymbol x||$，可以通过点积$\boldsymbol {x^Tx}$计算。

$\boldsymbol{x^Ty}=||\boldsymbol x||_2||\boldsymbol y||_2\cos\theta$

平方$L^2$范数：对每个元素的倒数只取决于对应元素，而不平方会与整个向量相关但在原点附近增长缓慢。

$L^1$范数：区分恰好是0的元素和接近于0的元素。表示非零元素数目。

$||\boldsymbol x||_1=\sum_i|x_i|$

最大范数：表示向量中具有最大幅值的元素的绝对值。

$||\boldsymbol x||_\infty=\max_i|x_i|$

Frobenius范数：衡量矩阵大小

$||\boldsymbol A||_ F=\sqrt{\sum_{i,j}A^2_{i,j},}$

特殊类型的矩阵和向量

对角矩阵：只在对角线上含有非零元素

$diag(\boldsymbol v)$：对角元素由向量中元素构成

对称矩阵：转置和自己相等

单位向量：具有单位范数的向量

$||\boldsymbol x||_ 2=1$

正交：$\boldsymbol {x^Ty}=0$

标准正交：正交且范数为1

正交矩阵：行向量和列向量分别标准正交的方阵，求逆代价小

$\boldsymbol{A^TA}=\boldsymbol{AA^T}=\boldsymbol I\\\\ \boldsymbol{A^{-1}=\boldsymbol{A^T}}$

特征分解

特征分解：将矩阵分解成一组特征向量和特征值。

特征向量：

$\boldsymbol {Av}=\lambda\boldsymbol v$

特征分解：

$\boldsymbol A=\boldsymbol Vdiag(\boldsymbol \lambda)\boldsymbol {V^{-1}}$

其中$\boldsymbol V=[v^{(1)},…,v^{(n)}]$，$\boldsymbol\lambda=[\lambda_1,…,\lambda_n]$

每一个实对称矩阵都可以分解成实特征向量和实特征值：

$\boldsymbol A=\boldsymbol {Q\Lambda Q^T}$

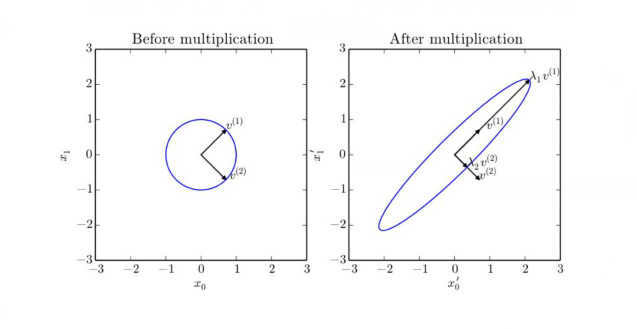
其中Q是A特征向量构成的正交矩阵，可以将A看作沿方向$\boldsymbol v^{(i)}$延伸$\lambda_i$倍的空间。

矩阵是奇异的当且仅当含有0特征值。

这咋整啊

奇异值分解

奇异值分解（SVD）：奇异向量+奇异值

每个实数矩阵都有一个奇异值分解，但不一定都有特征值分解。

$\boldsymbol A=\boldsymbol {UDV^T}$

$\boldsymbol A:m\times n$

$\boldsymbol U:m\times m$，正交矩阵，列向量为左奇异向量

$\boldsymbol D:m\times n$，对角矩阵（不一定是方阵），对角线上元素为奇异值

$\boldsymbol V:n\times n$，列向量为右奇异向量

左奇异向量是$\boldsymbol {AA^T}$的特征向量，右奇异向量是$\boldsymbol {A^TA}$的特征向量，非零奇异值是$\boldsymbol {AA^T}$和$\boldsymbol {A^TA}$特征值的平方根。

Moore-Penrose 伪逆

对于非方阵，没有逆矩阵。

$\boldsymbol A^+=\boldsymbol {VD^+U^T}$

其中，U,D和V是A奇异值分解后得到的矩阵，$D^+$是D非零元素取倒数之后再转置得到。

当矩阵列数多于行数时，$x=\boldsymbol A^+y$是方程中L2范数最小的一个。

当矩阵行数多于列数时，伪逆得到的x使得Ax和y的欧几里得距离$||\boldsymbol {Ax-y}||_
2$最小。

迹运算

$Tr(\boldsymbol A)=\sum_iA_{i,i}$

Frobenius范数：

$||\boldsymbol A||_ F=\sqrt{\sum_{i,j}A^2_{i,j},}=\sqrt{Tr(\boldsymbol{AA^T})}$

转置前后迹不变

多个矩阵相乘得到方阵的迹，将最后一个挪到最前面之后迹不变。

$Tr(\prod^n_{i=1}\boldsymbol F^{(i)})=Tr(\boldsymbol F^{(n)}\prod^{n-1}_ {i=1}\boldsymbol F^{(i)})$

对于标量：a=Tr(a)。

行列式

行列式：$det(\boldsymbol A)$，将方阵映射到实数的函数。

行列式等于矩阵特征值的乘积。

行列式绝对值衡量矩阵参与矩阵乘法后空间扩大或缩小了。

主成分分析

主成分分析：PCA，对空间中的m个点进行有损压缩，希望损失的精度尽可能少。

方法：用低维表示，即存在l小于n。

找到一个编码函数，根据输入返回编码，$f(\boldsymbol x)=c$，一个解码函数，给定编码重构输入，$\boldsymbol{x} \approx g(f(\boldsymbol{x}))$

定义解码矩阵$\boldsymbol{D} \in \mathbb{R}^{n \times l}$，$g(\boldsymbol c)=\boldsymbol{Dc}$

限制$\boldsymbol D$的所有列向量具有单位范数且彼此正交。

为得到最优编码 $\boldsymbol c^ $ ，最小化原始输入向量 $ \boldsymbol x $ 和重构向量 $ g(\boldsymbol c^ )$之间的距离，使用平方$L^2$范数：

$c^{ * }=\arg \min _ {c}\|x-g(c)\|_ {2}^{2}$

最小化函数化简：

$\begin{aligned} &(\boldsymbol x-g(\boldsymbol c))^{\top}(\boldsymbol x-g(\boldsymbol c))\\\\ =&\boldsymbol x^{\top} \boldsymbol x-\boldsymbol x^{\top} g(\boldsymbol c)-g(\boldsymbol c)^{\top} \boldsymbol x+g(\boldsymbol c)^{\top} g(\boldsymbol c)\\\\ =&\boldsymbol{x}^{\top} \boldsymbol{x}-2 \boldsymbol{x}^{\top} g(\boldsymbol{c})+g(\boldsymbol{c})^{\top} g(\boldsymbol{c}) \end{aligned}$

其中标量$g(\boldsymbol c)^{\top} \boldsymbol x$的转置等于本身。

第一项不依赖于c，因此：

$\begin{aligned} \boldsymbol c^{ * }&=\underset{c}{\arg \min }-2 \boldsymbol{x}^{\top} g(\boldsymbol{c})+g(\boldsymbol{c})^{\top} g(\boldsymbol{c})\\\\ &=\underset{c}{\arg \min }-2 \boldsymbol x^{\top} \boldsymbol D \boldsymbol c+\boldsymbol c^{\top} \boldsymbol D^{\top} \boldsymbol D c \\\\ &=\underset{c}{\arg \min }-2\boldsymbol x^{\top}\boldsymbol D\boldsymbol c+\boldsymbol c^{\top} \boldsymbol I_{l} \boldsymbol c\\\\ &=\underset{c}{\arg \min }-2 \boldsymbol{x}^{\top} \boldsymbol{D} \boldsymbol{c}+\boldsymbol{c}^{\top} \boldsymbol{c} \end{aligned}$

通过向量微积分求解优化：

$\begin{array}{c} \nabla_{c}\left(-2 \boldsymbol{x}^{\top} \boldsymbol{D} \boldsymbol{c}+\boldsymbol{c}^{\top} \boldsymbol{c}\right)=0 \\\\ -2 \boldsymbol{D}^{\top} \boldsymbol{x}+2 \boldsymbol{c}=0 \\\\ \boldsymbol{c}=\boldsymbol{D}^{\top} \boldsymbol{x} \end{array}$

因此使用编码函数：

$f(\boldsymbol x)=\boldsymbol D^{\top} \boldsymbol x$

根据矩阵乘法定义PCA重构操作：

$r(\boldsymbol{x})=g(f(\boldsymbol{x}))=\boldsymbol{D} \boldsymbol{D}^{\top} \boldsymbol{x}$

挑选编码矩阵D，最小化所有维数和所有点上的误差矩阵的F范数：

$\boldsymbol{D}^{ * }=\underset{\boldsymbol{D}}{\arg \min } \sqrt{\sum_{i, j}\left(x_{j}^{(i)}-r\left(\boldsymbol{x}^{(i)}\right)_ {j}\right)^{2}} \text { subject to } \boldsymbol{D}^{\top} \boldsymbol{D}=\boldsymbol{I}_ {l}$

首先考虑$l=1$，此时$\boldsymbol D$为向量$\boldsymbol d$：

$\boldsymbol d^{* }=\underset{\boldsymbol d}{\arg \min } \sum_{i}\left\|\boldsymbol x^{(i)}-\boldsymbol d \boldsymbol d^{\top} \boldsymbol x^{(i)}\right\|_ {2}^{2} \text { subject to }\|\boldsymbol d\|_ {2}=1$

将标量写在左边：

$\begin{aligned} \boldsymbol d^{* }=\underset{\boldsymbol d}{\arg \min } \sum_ {i}\left\|\boldsymbol x^{(i)}-\boldsymbol d^{\top} \boldsymbol x^{(i)} \boldsymbol d\right\|_ {2}^{2} \text { subject to }\|\boldsymbol d\|_ {2}=1\\\\ \boldsymbol d^{* }=\underset{\boldsymbol d}{\arg \min } \sum_{i}\left\|\boldsymbol x^{(i)}-\boldsymbol x^{(i) \top}\boldsymbol d\boldsymbol d\right\|_ {2}^{2} \text { subject to }\|\boldsymbol d\|_ {2}=1 \end{aligned}$

用矩阵表示，$\boldsymbol{X} \in \mathbb{R}^{m \times n}$，其中$\boldsymbol{X}_{i, :}=\boldsymbol{x}^{(i)^{\top}}$，因此：

$\begin{aligned} \boldsymbol d^{* }=\underset{\boldsymbol d}{\arg \min }\left\|\boldsymbol X-\boldsymbol {X d d^{\top}}\right\|_ {F} ^{2} \text { subject to }\boldsymbol{ d^{\top} d}=1 \end{aligned}$

化简F范数：

$\begin{aligned}& \underset{\boldsymbol d}{\arg \min }\left\|\boldsymbol{X}-\boldsymbol{X} \boldsymbol d \boldsymbol{d}^{\top}\right\|_ {F}^{2} \\\\=&\underset{\boldsymbol d}{\arg \min } \operatorname{Tr}\left(\left(\boldsymbol{X}-\boldsymbol{X} \boldsymbol d \boldsymbol{d}^{\top}\right)^{\top}\left(\boldsymbol{X}-\boldsymbol{X} \boldsymbol d \boldsymbol{d}^{\top}\right)\right)\\\\=&\underset{\boldsymbol d}{\arg \min } \operatorname{Tr}\left(\boldsymbol{X}^{\top} \boldsymbol{X}-\boldsymbol{X}^{\top} \boldsymbol{X} {\boldsymbol {d d^{\top}-d} }\boldsymbol{d}^{\top} \boldsymbol{X}^{\top} \boldsymbol{X}+\boldsymbol d \boldsymbol{d}^{\top} \boldsymbol{X}^{\top} \boldsymbol{X} \boldsymbol d \boldsymbol{d}^{\top}\right) \\\\=&\underset{\boldsymbol d}{\arg \min } \operatorname{Tr}\left(\boldsymbol{X}^{\top} \boldsymbol{X}\right)-\operatorname{Tr}\left(\boldsymbol{X}^{\top} \boldsymbol{X} \boldsymbol d \boldsymbol{d}^{\top}\right)-\operatorname{Tr}\left(\boldsymbol d \boldsymbol{d}^{\top} \boldsymbol{X}^{\top} \boldsymbol{X}\right)+\operatorname{Tr}\left(\boldsymbol d \boldsymbol{d}^{\top} \boldsymbol{X}^{\top} \boldsymbol{X} \boldsymbol d \boldsymbol{d}^{\top}\right) \\\\=&\underset{\boldsymbol d}{\arg \min }-\operatorname{Tr}\left(\boldsymbol{X}^{\top} \boldsymbol{X} \boldsymbol d \boldsymbol{d}^{\top}\right)-\operatorname{Tr}\left(\boldsymbol d \boldsymbol{d}^{\top} \boldsymbol{X}^{\top} \boldsymbol{X}\right)+\operatorname{Tr}\left(\boldsymbol d \boldsymbol{d}^{\top} \boldsymbol{X}^{\top} \boldsymbol{X} \boldsymbol d \boldsymbol{d}^{\top}\right)\\\\=&\underset{\boldsymbol d}{\arg \min }-2 \operatorname{Tr}\left(\boldsymbol{X}^{\top} \boldsymbol{X} \boldsymbol{d} \boldsymbol{d}^{\top}\right)+\operatorname{Tr}\left(\boldsymbol{d} \boldsymbol{d}^{\top} \boldsymbol{X}^{\top} \boldsymbol{X} \boldsymbol{d} \boldsymbol{d}^{\top}\right)\\\\=&\underset{\boldsymbol d}{\arg \min }-2 \operatorname{Tr}\left(\boldsymbol{X}^{\top} \boldsymbol{X} \boldsymbol{d} \boldsymbol{d}^{\top}\right)+\operatorname{Tr}\left(\boldsymbol{X}^{\top} \boldsymbol{X} \boldsymbol{d} \boldsymbol{d}^{\top} \boldsymbol{d} \boldsymbol{d}^{\top}\right)（循环改变迹运算中相乘矩阵的顺序不影响结果）\end{aligned}$

考虑约束条件：

$\begin{aligned} &\underset{\boldsymbol d}{\arg \min }-2 \operatorname{Tr}\left(\boldsymbol{X}^{\top} \boldsymbol{X} \boldsymbol{d} \boldsymbol{d}^{\top}\right)+\operatorname{Tr}\left(\boldsymbol{X}^{\top} \boldsymbol{X} \boldsymbol{d} \boldsymbol{d}^{\top} \boldsymbol{d} \boldsymbol{d}^{\top}\right) \text { subject to } \boldsymbol{d}^{\top} \boldsymbol{d}=1\\\\ =&\underset{\boldsymbol d}{\arg \min }-2 \operatorname{Tr}\left(\boldsymbol{X}^{\top} \boldsymbol{X} d \boldsymbol{d}^{\top}\right)+\operatorname{Tr}\left(\boldsymbol{X}^{\top} \boldsymbol{X} \boldsymbol{d} \boldsymbol{d}^{\top}\right) \text { subject to } \boldsymbol{d}^{\top} \boldsymbol{d}=1\\\\ =&\underset{\boldsymbol d}{\arg \min }-\operatorname{Tr}\left(\boldsymbol{X}^{\top} \boldsymbol{X} \boldsymbol{d} \boldsymbol{d}^{\top}\right) \text { subject to } \boldsymbol{d}^{\top} \boldsymbol{d}=1\\\\ =&\underset{\boldsymbol d}{\arg \max } \operatorname{Tr}\left(\boldsymbol{X}^{\top} \boldsymbol{X} \boldsymbol{d} \boldsymbol{d}^{\top}\right) \text { subject to } \boldsymbol{d}^{\top} \boldsymbol{d}=1\\\\ =&\underset{\boldsymbol d}{\arg \max } \operatorname{Tr}\left(\boldsymbol{d}^{\top} \boldsymbol{X}^{\top} \boldsymbol{X} \boldsymbol{d}\right) \text { subject to } \boldsymbol{d}^{\top} \boldsymbol{d}=1 \end{aligned}$

因此最优的$\boldsymbol d$是$\boldsymbol{X^{\top}X}$最大的特征值对应的特征向量。