主席树：可持久化线段树

发表于 | 更新于:

主席树好难啊qaq

前置技能

离散化

此坑待填

权值线段树

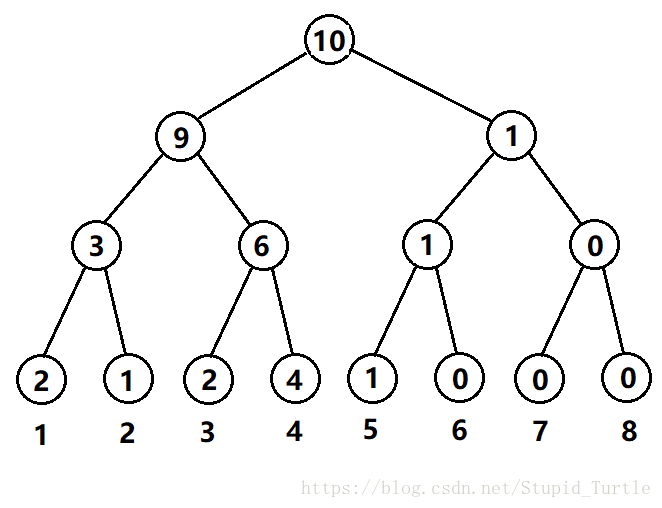
权值线段树的每个节点用来维护在[l,r]区间内数的个数，通常用来求k大值，时间复杂度为log n。
比如对于长度为10的数组[1,1,2,3,3,4,4,4,4,5]，我们可以构造权值线段树如下。

具体操作同普通的线段树qwq……

下面是主席树

主席树是一种可持久化线段树，对于每次操作，可以保留历史版本，便于查询，是一棵权值线段树每次复制一条链得到。
比如对于最经典的求区间k大值问题：
对于长度为10的数组a，如果我们只用权值线段树的话，那么为了求[l,r]区间的k大值，我们需要建立10棵权值线段树，分别用Ti记录插入a[i]后的权值线段树。
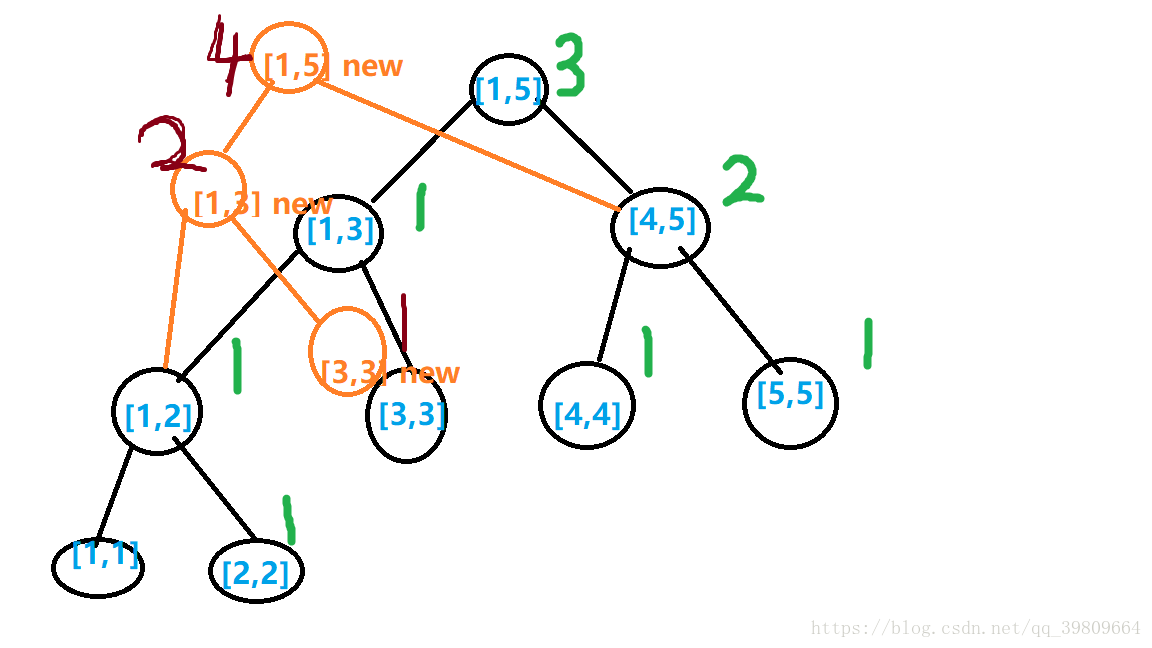
但是这样会浪费掉很大空间，因为每插入一个a[i]，只会有一条链的值发生变化，所以我们可以只建立一棵权值线段树，然后每插入一个a[i]，就复制需要改变的那一条链，将它与剩余节点相连，假装是一棵新建的树……

如图，黄色的圈就是插入一个值的时候，将对应的链复制过来并修改，假装是一棵新的树Ti。
以此类推，如果数组有n个节点的话，这样下来就会保留n个版本，也就是n棵假装的树。
每次查询[l,r]区间的k大值，就可以递归找使Tl和Tr两棵树的节点个数差为k的区间。
头疼的一批，顶不住了，不如上板子。
（板子并不是k大值
（注意update函数中的&

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56

#include<cstdio>
#include<iostream>
using namespace std;
const int N=1e5+10;
int root[N],ls[40*N],rs[40*N],sum[40*N];
int n,m,sz;
inline int read()
{
    char ch=getchar();
    while(!(ch>='0'&&ch<='9'))ch=getchar();
    int x=0;
    while(ch>='0'&&ch<='9'){x=x*10+(ch-'0');ch=getchar();}
    return x;
}
void update(int l,int r,int x,int &y,int v)
{
    y=++sz;
    sum[y]=sum[x]+1;//递归过程就对应着改
    if(l==r)return;
    ls[y]=ls[x];rs[y]=rs[x];//先赋成一样的
    int mid=(l+r)>>1;
    if(v<=mid)update(l,mid,ls[x],ls[y],v);//递归进去改ls[y]，引用之后ls[y]也对应了改变
    else update(mid+1,r,rs[x],rs[y],v);
}
int que(int L,int R)//L R传进来两棵树
{
    int l=1,r=n,mid,x,y,tmp=(R-L+1)>>1;
    x=root[L-1];y=root[R];
    while(l!=r)
    {
        if(sum[y]-sum[x]<=tmp)return 0;
        mid=(l+r)>>1;
        if(sum[ls[y]]-sum[ls[x]]>tmp)//左子树
        {r=mid;x=ls[x];y=ls[y];}
        else if(sum[rs[y]]-sum[rs[x]]>tmp)//右子树
        {l=mid+1;x=rs[x];y=rs[y];}
        else return 0;
    }
    return l;
}
int main()
{
    n=read();m=read();
    for(int i=1;i<=n;i++)
    {
        int x;x=read();
        update(1,n,root[i-1],root[i],x);
    }
    for(int i=1;i<=m;i++)
    {
        int l,r;l=read();r=read();
        printf("%d\n",que(l,r));
    }
    return 0;
}